
So, if you want to consider clockwise angles positive, just use a left-handed coordinate system (where $x$ increases right, and $y$ downwards).ĭo remember to state your preferred handedness, though most mathematicians et cetera assume a right-handed coordinate system unless stated otherwise. The underlying reason why we use $\cos$ for $x$ axis, and $\sin$ for $y$ axis, comes from Euler, and complex numbers in particular: It is just that most humans are predominantly right-handed, and that does seem to permeate our culture in very subtle ways.) (Note that by rotating the coordinate system 180°, $x$ axis increases left, and $y$ down I do not recall seeing this convention anywhere in practice, but I guess it would be just as natural to predominantly left-handed people. Such coordinate systems are often used in e.g. In a left-handed coordinate system, $y$ axis increases down, and $x$ axis right, and positive angles are indeed clockwise.
CLOCKWISE DIRECTION HOW TO
I'm afraid I don't know how to answer your second question.Positive angles are counterclockwise only in right-handed coordinate systems, where $y$ axis increases upwards, and $x$ axis right.

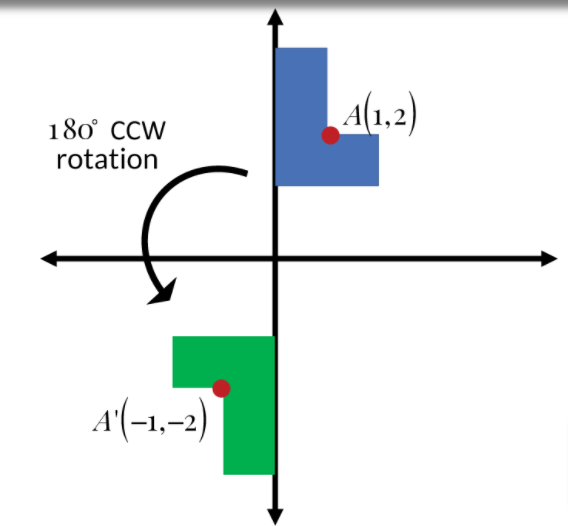
In physics, the counterclockwise direction is defined as positive and clockwise is negative for rotational variables. These terms refer to the movement of hands on a clock (see Figure 5). The equation is using a positive x point, rotating down to a negative x point, like the first example I used. The direction of rotation can be clockwise (cw) or counterclockwise (ccw). This is because the point was originally on a negative x point, so now it will be a positive x. Now wait a second, why isn't the 8 a negative? After all, the equation is: Like the pattern states, the coordinates will flip (8,5). This time, I'll use coordinates (-5,8) as my point. Let's take another example, still rotating it by -90 around the origin. The original x point was on the positive side, so when you rotate it, it's going to the negative x. *Why does the x become negative?* That's because the point going down into the negative quadrant. The point (-3,6), is among one of those points. *Why do the coordinates flip?* Imagine there's a circle in the grid, telling you all the points of where (6,3) can be rotated to. Following the pattern of the equation, it becomes (-3,6). I'm going to rotate that point -90 (clockwise) around the origin. Let's start by using coordinates (6,3) as an example. It's definitely a bit puzzling, so here's what I gathered: Remember! A negative and a negative gives a positive! So if we rotate another 180 degrees we go from (-2, -1) to (2, 1)Īnd if we have another point like (-3, 2) and rotate it 180 degrees, it will end up on (3, -2) So from 0 degrees you take (x, y) and make them negative (-x, -y) and then you've made a 180 degree rotation. When you rotate by 180 degrees, you take your original x and y, and make them negative. If you have a point on (2, 1) and rotate it by 180 degrees, it will end up at (-2, -1)
We do the same thing, except X becomes a negative instead of Y. If you understand everything so far, then rotating by -90 degrees should be no issue for you. Our point is as (-2, -1) so when we rotate it 90 degrees, it will be at (1, -2)Īnother 90 degrees will bring us back where we started. What about 90 degrees again? Same thing! But remember that a negative and a negative gives a positive so when we swap X and Y, and make Y negative, Y actually becomes positive. Our point is at (-1, 2) so when we rotate it 90 degrees, it will be at (-2, -1) What if we rotate another 90 degrees? Same thing. So from 0 degrees you take (x, y), swap them, and make y negative (-y, x) and then you have made a 90 degree rotation. When you rotate by 90 degrees, you take your original X and Y, swap them, and make Y negative. If you have a point on (2, 1) and rotate it by 90 degrees, it will end up at (-1, 2) In case the algebraic method can help you:


 0 kommentar(er)
0 kommentar(er)
